Penerapan Simulink Untuk Simulasi

Penerapan Simulink Untuk Simulasi

PEMODELAN DAN SIMULASI

Sistem adalah kumpulan obyek yang saling berinteraksi dan bekerja sama untuk mencapai tujuan logis dalam suatu lingkungan yang kompleks. Obyek yang menjadi komponen dari sistem dapat berupa obyek terkecil dan bisa juga berupa sub-sistem atau sistem yang lebih kecil lagi. Dalam definisi ini disertakan elemen lingkungan karena lingkungan sistem memberikan peran yang sangat penting terhadap perilaku sistem itu. Bagaimana komponen-komponen sistem itu berinteraksi, hal itu adalah dalam rangka mengantisipasi lingkungan.

Mengamati sistem bukan hanya mendefinisikan komponen-komponen pendukung sistem, tetapi lebih dari dari itu harus pula mengetahui perilaku dan variabel-variabel yang ada di dalamnya. Paling tidak analisis terhadap sistem harus dapat membuat konsepsi tentang sistem itu. Ada beberapa cara untuk dapat merancang, menganalisis dan mengoperasikan suatu sistem. Obyek penelitian biasanya merupakan suatu sistem dengan kerumitan-kerumitan yang sangat kompleks sehingga memerlukan pengabstraksian. Salah satunya adalah dengan melakukan pemodelan, membuat model dari sistem tersebut.

Istilah pemodelan adalah terjemahan bebas dari istilah modelling. Untuk menghindari berbagai pengertian atau penafsiran yang berbeda-beda, maka istilah pemodelan dapat diartikan sebagai suatu rangkaian aktivitas pembuatan model. Sebagai landasan untuk lebih memahami pengertian pemodelan maka diperlukan suatu penelaahan tentang model secara spesifik ditinjau dari pendekatan sistem.

Dalam konteks terminologi penelitian operasional (operation research), secara umum model didefinisikan sebagai suatu perwakilan atau abstraksi dari suatu obyek atau situasi aktual. Model melukiskan hubungan-hubungan langsung dan tidak langsung serta kaitan timbal-balik dalam terminologi sebab akibat. Oleh karena suatu model adalah abstraksi dari realita, maka pada wujudnya lebih sederhana dibandingkan dengan realita yang diwakilinya. Model dapat disebut lengkap apabila dapat mewakili berbagai aspek dari realita yang sedang dikaji. Model adalah alat yang sangat berguna untuk menganalisis maupun merancang sistem. Sebagai alat komunikasi yang sangat efisien, model dapat menunjukkan bagaimana suatu operasi bekerja dan mampu merangsang untuk berpikir bagaimana meningkatkan atau memperbaikinya. Model didefinisikan sebagai suatu deskripsi logis tentang bagaimana sistem bekerja atau komponen-komponen berinteraksi.

Salah satu syarat pokok untuk mengembangkan model adalah menemukan peubah-peubah apa yang penting dan tepat. Penemuan peubah-peubah ini sangat erat hubungannya dengan pengkajian hubungan-hubungan yang terdapat di antara peubah-peubah. Teknik kuantitatif seperti persamaan regresi dan simulasi digunakan untuk mempelajari keterkaitan antar peubah dalam sebuah model.

Memang dimungkinkan untuk dapat merancang-bangun dengan baik berbagai model sistem tanpa matematik, dan /atau mengetahui matematika tanpa analisis sistem. Namun demikian, perumusan matematika yang terpilih dapat mempermudah pengkajian sistem, yang pada umumnya merupakan suatu kompleksitas. Sifat universalitas dari matematik dan notasi-notasinya akan memperlancar komunikasi dan transfer metode yang dikembangkan di suatu negara atau bidang ilmu tertentu ke bidang lainnya.

Kebanyakan para pengguna analisis sistem menjumpai kesukaran untuk mengimplementasikan notasi-notasi matematika ke dalam format konsepsi disiplin ilmunya. Mereka kemudian memilih alternatif pembuatan model konsepsi (conceptual model) yang sifatnya informal karena terasa lebih mudah. Bagaimanapun juga, para ahli sistem berpendapat bahwa keuntungan lebih besar dibandingkan dengan biaya yang diperlukan dalam mengkaji permasalahan penelitian secara matematis. Hal ini disebabkan adanya daya guna yang berlipat ganda pada proses rancang bangun dan analisis dalam bentuk bahasa matematika yang sangat penting dalam teori ekonomi, keteknikan, ilmu alam hingga ilmu-ilmu sosial. Meskipun teknik-tekniknya sangat beragam dan filosofinya masih dipandang kontraversi namun ide dasarnya adalah sederhana yaitu menjabarkan keterkaitan-keterkaitan yang ada dalam dunia nyata menjadi operasi-operasi matematis.

Dengan membuat model dari suatu sistem maka diharapkan dapat lebih mudah untuk melakukan analisis. Hal ini merupakan prinsip pemodelan, yaitu bahwa pemodelan bertujuan untuk mempermudah analisis dan pengembangannya. Melakukan pemodelan adalah suatu cara untuk mempelajari sistem dan model itu sendiri dan juga bermacam-macam perbedaan perilakunya.

Ada beberapa langkah di dalam mempelajari sebuah sistem. Secara lengkap digambarkan dengan diagram / gambaran seperti dibawah ini :

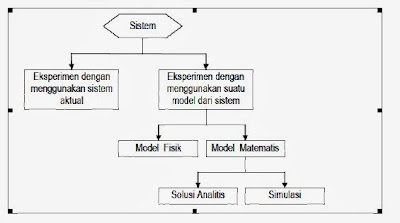
Gambaran Dari Aneka Cara Mempelajari Sebuah Sistem :

Jika suatu sistem secara fisik memungkinkan dan tidak memakan biaya yang besar untuk dioperasikan sesuai dengan kondisi (scenario) yang kita inginkan maka cara ini merupakan cara yang terbaik karena hasil dari eksperimen ini benar-benar sesuai dengan sistem yang dikaji. Namun sistem seperti itu jarang sekali ada dan penghentian operasi sistem untuk keperluan eksperimen akan memakan biaya yang sangat besar. Selain itu untuk sistem yang belum ada atau sistem yang masih dalam rancangan maka eksperimen dengan sistem aktual jelas tidak bisa dilakukan sehingga satu-satunya cara adalah dengan menggunakan model sebagi representasi dari sistem aktual.

Model fisik atau ikonik pada hakekatnya merupakan perwakilan fisik dari beberapa hal, baik dalam bentuk ideal maupun dalam skala yang berbeda. Model ikonik ini mempunyai karakteristik yang sama dengan hal yang diwakilinya, dan terutama amat sesuai untuk menerangkan kejadian pada waktu yang spesifik. Model ikonik dapat berdimensi dua (foto, peta, cetak-biru) atau tiga dimensi (prototipe mesin, alat, dan lainnya). Apabila model berdimensi lebih dari tiga tidak mungkin lagi dikonstruksi secara fisik sehingga diperlukan kategori model simbolik.

Model fisik mengambil dari sebagian sifat fisik dari hal-hal yang diwakilinya, sehingga menyerupai sistem yang sebenarnya namun dalam skala yang berbeda. Walaupun jarang dipakai, model ini cukup berguna dalam rekayasa sistem.

Pada hakekatnya, ilmu sistem memusatkan perhatian pada model matematis atau model simbolik sebagai perwakilan dari realita yang dikaji. Format model simbolik dapat berupa bentuk angka, simbol dan rumus. Jenis model simbolik yang umum dipakai adalah suatu persamaan (equation).

Bentuk persamaan adalah tepat, singkat dan mudah dimengerti. Simbol persamaan tidak saja mudah dimanipulasi dibandingkan dengan kata-kata, namun juga lebih cepat dapat ditanggap maksudnya. Suatu persamaan adalah bahasa yang universal pada penelitian operasional dan ilmu sistem, dimana di dalamnya digunakan suatu logika simbolis.

Dalam mempelajari ilmu sistem diperlukan suatu pengertian yang mendasar tentang simbol-simbol matematika; karena kalau tidak demikian akan menambah kompleksitas dari konsep pengkajian itu sendiri. Bagaimanapun juga sebagaimana mempelajari suatu hal maka kunci dari kelancaran dan pemahamannya adalah frekuensi latihan aplikasinya. Dengan demikian diharapkan para pengguna dapat secara efisien menangkap arti dari setiap notasi matematis yang disajikan. Misalnya , notasi ai dapat diartikan faktor peubah a, dan Aij dapat digambarkan sebagai Tabel matriks peubah A dengan baris i dan kolom j.

Dalam penelitian, model matematis lebih sering dipakai jika dibandingkan dengan model fisik. Pada model matematis, sistem direpresentasikan sebagai hubungan logika dan hubungan kuantitatif untuk kemudian dimanipulasi supaya dapat dilihat bagaimana sistem bereaksi.

Setelah model matematis berhasil dirumuskan, model tersebut dipelajari kembali apakah model yang telah dikembangkan dapat menjawab pertanyaan yang berkaitan dengan tujuan mempelajari sistem. Jika model yang dibentuk cukup sederhana, maka relasi-relasi matematisnya dapat digunakan untuk mencari solusi analitis. Jika solusi analitis bisa diperoleh dengan cukup mudah dan efisien, maka sebaiknya diigunakan solusi analitis karena metode ini mampu memberikan solusi yang optimal terhadap masalah yang dihadapi. Tetapi seringkali model terlalu kompleks sehingga sangat sulit untuk diselesaikan dengan metoda-metoda analitis, maka model tersebut dapat dipelajari dengan simulasi. Simulasi tidak menjamin memberikan hasil yang optimal melainkan dijamin bahwa hasilnya mendekati optimal.

Pada dasarnya model simulasi dikelompokkan dalam tiga dimensi yaitu [Law and Kelton, 1991] :

Model Simulasi Statis dengan Model Simulasi Dinamis.

Model simulasi statis digunakan untuk mempresentasikan sistem pada saat tertentu atau sistem yang tidak terpengaruh oleh perubahan waktu. Sedangkan model simulasi dinamis digunakan jika sistem yang dikaji dipengaruhi oleh perubahan waktu.

Model Simulasi Deterministik dengan Model Simulasi Stokastik.

Jika model simulasi yang akan dibentuk tidak mengandung variabel yang bersifat random, maka model simulasi tersebut dikatakan sebagi simulasi deterministik. Pada umumnya sistem yang dimodelkan dalam simulasi mengandung beberapa input yang bersifat random, maka pada sistem seperti ini model simulasi yang dibangun disebut model simulasi stokastik.

Model simulasi Kontinu dengan Model Simulasi Diskret.

Untuk mengelompokkan suatu model simulasi apakah diskret atau kontinyu, sangat ditentukan oleh sistem yang dikaji. Suatu sistem dikatakan diskret jika variabel sistem yang mencerminkan status sistem berubah pada titik waktu tertentu, sedangkan sistem dikatakan kontinyu jika perubahan variabel sistem berlangsung secara berkelanjutan seiring dengan perubahan waktu.

Dengan melakukan studi simulasi maka dalam waktu singkat dapat ditentukan keputusan yang tepat serta dengan biaya yang tidak terlalu besar karena semuanya cukup dilakukan dengan komputer. Pendekatan simulasi diawali dengan pembangunan model sistem nyata. Model tersebut harus dapat menunjukkan bagaimana berbagai komponen dalam sistem saling berinteraksi sehingga benar-benar menggambarkan perilaku sistem. Setelah model dibuat maka model tersebut ditransformasikan ke dalam program komputer.

Penerapan simulasi dalam program komputer disebut sebagai Simulink. Simulink adalah salah satu bagian dari MatLab (Matriks Laboratory) Program. Simulink dapat digunakan untuk mensimulasi sistem artinya mengamati dan menganalisa perilaku dari tiruan sistem. Tiruan sistem diharapkan mempunyai perilaku yang sangat mirip dengan sistem fisik. Jika digunakan dengan benar, simulasi akan membantu proses analisis dan desain sistem.

TAHAPAN DALAM PEMODELAN

Para ahli penelitian operasional dan ilmu sistem telah memberikan konsepsi dan teknik pemodelan sistem. Para ahli ini menyarankan untuk mengawali pemodelan dengan penguraian seluruh komponen yang akan mempengaruhi efektivitas dari operasi sistem. Setelah daftar komponen tersebut lengkap, langkah selanjutnya adalah penyaringan komponen mana yang akan dipakai dalam pengkajian tersebut. Hal ini umumnya sulit karena adanya interaksi antar peubah yang seringkali menyulitkan isolasi suatu peubah. Peubah yang dipandang tidak penting ternyata bisa saja mempengaruhi hasil studi setelah proses pengkajian selesai. Untuk menghindarkan hal ini, diperlukan percobaan pengujian data guna memilih komponen-komponen yang kritis. Setelah itu dibentuk gugus persamaan yang dapat dievaluasi dengan merubah-rubah komponen tertentu dalam batas-batas yang diperkenankan. Salah satu contoh pemodelan seperti ini adalah Program Linear (Linear Programming) dan Program Dinamik (Dynamic Programming).

Dalam konteks pendekatan sistem, tahap-tahap pemodelannya lebih kompleks namun relatif terlalu beragam, baik ditinjau dari jenis sistem ataupun tingkat kecanggihan model. Manetsch dan Park (1984) mengembangkan tahap pemodelan abstrak ini sebagai bagian dari pendekatan sistem.

Pemodelan abstrak menerima input berupa alternatif sistem yang layak. Proses ini membentuk dan mengimplementasikan model-model matematika yang dimanfaatkan untuk merancang program terpilih yang akan dipraktekkan di dunia nyata pada tahap berikutnya. Output utama dari tahap ini adalah deskripsi terinci dari keputusan yang diambil berupa perencanaan, pengendalian atau kebijakan lainnya.

IMPLEMENTASI KOMPUTER

Pemakaian komputer sebagai pengolah data, penyimpan data dan komunikasi informasi tidak dapat diabaikan dalam pendekatan system, model abstrak diwujudkan dalam berbagai bentuk persamaan, diagram alir dan diagram blok. Tahap ini seolah-olah membentuk model dari suatu model, yaitu tingkat abstraksi lain yang ditarik dari dunia nyata. Hal yang penting di sini adalah memilih teknik dan bahasa komputer yang digunakan untuk implementasi model. Masalah ini akan mempengaruhi :

1. Ketelitian dari hasil komputasi

2. Biaya operasi model

3. Kesesuaian dengan komputer yang tersedia

4. Efektifitas dari proses pengambilan keputusan yang akan menggunakan hasil pemodelan tersebut.

Setelah program komputer dibuat dan format input /output telah dirancang secara memadai, maka sampailah pada tahap pembuktian (verifikasi) bahwa model komputer tersebut mampu melakukan simulasi dari model abstrak yang dikaji. Pengujian ini mungkin berbeda dengan uji validitas model itu sendiri.

BAHASA SIMULASI

Pemrograman model simulasi, seperti yang disebutkan sebelumnya, dapat dilakukan menggunakan bahasa umum komputer (general purposes language) atau menggunakan bahasa simulasi. Ada beberapa bahasa simulasi, sehingga kita harus dapat melihat dan memahami kelebihan dan kekurangan dari masing-masingnya, sehingga kita melakukan pemilihan yang tepat saat kita perlu menggunakan bahasa simulasi.

Satu bahasa simulasi tidak dapat menjadi alat yang tepat untuk semua kasus permodelan simulasi. Kesuksesan analisis simulasi merupakan teknik campuran yang sangat tergantung pada keahlian dan keahlian analis. Elemen dan struktur bahasa komputer umum seperti Pascal atau FORTRAN, source codenya tidak dengan mudah dapat digunakan untuk memodelkan simulasi sistem. Msialnya, bahasa itu tidak menyediakan struktur data yang enak digunakan untuk pemrosesan kejadian, sementara hal ini merupakan elemen logis yang sangat penting dalam permodelan simulasi. Tidak ada perintah dalam FORTRAN misalnya yang dengan jelas menambah atau mengurangi antrian nasabah atau objek lainnya. Tidak ada perintah dalam FORTRAN yang mengakumulasikan jumlah objek dalam antrian dan menghitung rata-rata untuk menyediakan output statistik penting. Variabel waktu lanjut, yang penting dalam penjalanan model simulasi, juga tidak dapat ditemukan pada FORTRAN dan bahasa pemrograman umum lainnya.

Untuk memenuhi fungsi-fungsi di atas dan hal-hal penting lainnya dalam struktur model program komputer, kode pemrograman yang ekstensif, kompleks dan sulit didebug harus dibuat. Motivasi mengembangkan dan menggunakan bahasa simulasi berasal dari keinginan untuk mempersingkat waktu yagn dibutuhkan untuk mengembangkan mdoel valid yang relatif mudah didebug dan yang menyediakan output statistik yang dibutuhkan dalam pengambilan keputusan.

STRUKTUR BAHASA SIMULASI

Kiviat mendefinisikan struktur statis bahasa simulasi terdiri dari 3, yaitu identifikasi objek dan karakteristik objek, relasa antara objek dan penurunan objek. Struktur dinamisnya didefinisikan sebagai metode penambahan waktu simulasi.

Objek adalah komponen model dan sistem yang menjadi perhatian utama analisis, misalnya nasabah bank, komponen dalam lini perakitan, pengguna dalam sistem jaringan, dll. Bahasa yang berbeda memberikan definisi yang berbeda pada objek, misalnya dalam SIMAN disebut entities, dalam GPSS disebut transactions. Masing-masing objek dalam sistem yang sama mempunyai karakteristik yang berbeda. Nasabah bank misalnya, ada yang ingin melakukan penarikan, ada yang ingin melakukan setoran, dll. Pendefinisian karakteristik dalam bahasa yang berbeda juga berbeda. Karakteristik dalam SIMAN dan SIMSCRIPT misalnya didefinisikan sebagai attributes sedangkan dalam GPSS didefinisikan sebagai parameters, dan ada juga yang menggunakan definisi properties, dll.

Meskipun objek mempunyai karakteristik unik, untuk tujuan pemrosesan dalam model, ada baiknya karakteristik itu dikelompokkan. Setiap bahasa mempunyai mekanisme berbeda dalam melakukan pengelompokan ini. Bahkan dalam kasus sistem yang relatif kecil, mempertahankan semua objek dalam model selama penjalanan simulasi bisa tidak memungkinkan karena keterbatasan memori komputer. Akibatnya, alat untuk menurunkan objek ketika dibutuhkan dan menghapusnya jika sudah tidak dibutuhkan harus disediakan.

Cara setiap bahasa simulasi memfasilitasi ini sangat berbeda. Dalam beberapa kasus, mekanisme digunakan untuk menelusuri karakteristik akar bahasa kompiler darimana bahasa simulasi dikembangkan. Bahasa simulasi yang kurang dekat dengan konvensi struktur data dari kompiler tertentu menurunkan objek yagn sangat mirip dengan sudut pandang dunia bahasa. Sejalan dengan perbaikan kemampuan bahasa komputer umum (general purposes), bahasa simulasi khusus pada umumnya telah dikodean kembali seperti assembly, bahasa bebas mesin seperti C. Tetapi struktur awal penurunan objek tetap dalam bahasa simulasi.

Struktur statis bahasa simulasi menempatkan objek dalam ruangan model, yaitu dimana objek secara fisik ditempatkan dalam sistem. Struktur dinamis dibutuhkan untuk menempatkan objek dalam waktu dan memungkinkan keberlanjutan dari satu titik waktu ke titik lainnya. Seperti yang sudah dijelaskan dalam topik sebelumnya, ada dua pendekatan dasar yang digunakan dalam struktur dinamis, yaitu fixed-time step dan event-tracking.

Pendekatan fixed-time memeriksa sistem pada interval waktu tetap untuk menentukan apakah statusnya sudah berubah atau belum. Jika status masih sama, variabel waktu akan ditambahkan sebesar interval waktu-tetap. Meskipuns ecara logika pendekatan ini cukup sederhana, tapi metodenya sangat tidak efisien. Mungkin ada beberapa titik waktu dimana sistem tidak berubah statusnya, dan karenanya akan ada banyak pemeriksaan sistem yang tidak perlu. Akibatnya, tidak ada bahasa simulasi kejadian diskrit yang menggunakan pendekatan ini ke struktur dinamis.

Pendekatan event-tracking memeriksa sistem hanya jika ada perubahan status. Logika diamsukkan dalam model untuk menentukan kapan kejadian atau status sistem berubah, dan variabel waktu ditambahkan dengan tepat sampai titik sebelum sistem diperiksa. Logika yang dibutuhkan untuk melakukan ini lebih kompleks dibandingkan dengan langkah waktu-tetap, tetapi akan mengehmat waktu eksekusi model secara signifikan.

KARAKTERISTIK BAHASA SIMULASI

Struktur dinamis dan statis bahasa simulasi menyediakan kebutuhan jelas untuk mengeksekusi mode simulasi. Beberapa sifat bahasa simulasi lainnya dibutuhkan atau sangat diinginkan untuk penggunaan efektif analisis simulasi sebagai teknik pembantu pengambilan keputusan.

Pengembangan kode model. Kebanyakan bahasa simulasi masih membutuhkan pemasukan pernyataan kode untuk menciptakan kode model, tetapi kemampuan grafik mikrokomputer telah memungkinkan input grafik. Cara ini paling sesuai untuk bahasa yang fokus pada aliran objek melalui elemen atau blok model.

Debugging model. Begitu mode simulasi sudah dikodekan menggunakan bahasa simulasi yang dipilih, langkah selanjutnya adalah debugging kode sehingga model simulasi berjalan ke penghentian normal. Syntax errors (kesalahan sintaks) adalah permasalahan pertama dalam proses, dan analisis untuk mendeteksi ini sudah ditanam dalam bahasa simulasi umumnya. Kesulitan berikutnya yang dihadapi adalah perbaikan kesalahan selama eksekusi kode. Analisis bahasa simulasi umumnya tidak sesuai secara total dengan permasalahan ini. Setelah menemukan kesalahan seperti ini, program berhenti dan tidak memberikan alasan dalam bentuk logika model kenapa program berhenti.

Penurunan variabel acak. Untuk kebanyakan simulasi probabilistik, kemampuan mengekstrak sampel acak dari distribusi probabilitas tertentu sangat penting. Bahasa simulasi melakukannya dengan mudah.

Pengumpulan statistik. Penjalanan model simulasi tanpa mengumpulkan data ukuran kinerja sistem sama saja dengan tidak melakukan pengamatan pada sistem dunia nyata yang sedang berlangsung. Pengamat ada selama operasi sistem dunia nyata tetapi tidak mengamati dan mencatat apa yang terjadi. Bahasa simulasi harus memungkinkan pengguna dengan mudah menspesifikasikan beragam statistik yang dikumpulkan selama eksekusi model. Juga untuk membantu interpretasi output simulasi, kemampuan penggambaran grafik dan inferensi statistik diperlukan.

Disain percobaan. Karena analisis simulasi bersifat deskriptif, kesuksesan aplikasinya tergantung pada percobaan model. Rancangan percobaan efektif dan efisien benar-benar meningkatkan kualitas solusi yang didapatkan dari model simulasi.

Animasi grafis dan output dinamis. Kemampuan menggunakan bahasa simulasi pada mikrokomputer memungkinkan kemampuan grafis mesin ini untuk mengilustrasikan penjalanan mode simulasi atau outputnya. Ilustrasi objek yang mengalir melalui elemen model disebut sebagai animasi. Animasi biasanya menggunakan monitor berwarna dan dengan mudah mengenali simbol objek dan elemen model. Dengan mengamati aliran seperti itu, analisis dapat memperhatikan penyebaba permasalahan operasi dan dapat memperbaikinya. Animasi model akan memperlambat eksekusi model. Oleh akrena itu, animasi biasanya hanya dilakukan pada mikrokomputer cepat dengan memori besar.

PEMILIHAN BAHASA SIMULASI

Beberapa hal yang perlu diperhatikan dalam pemilihan bahasa simulasi adalah kemudahan untuk dipelajari, kemudahan menjelaskan pada orang yang bukan teknik, biaya, kode standar untuk semua komputer dan cakupan permasalahan yang dapat ditangani oleh bahasa. Pada umumnya, semakin mirip elemen bahasa simulasi dengan elemen dunia nyata, semakin mudah elemen itu dipelajari. Kemudahan menjelaskan fungsi bahasa simulasi ke manajer yang mengeluarkan dana untuk pembelian perangkat lunak dan yang tidak memahami secara teknis juga digunakan dalam memilih bahasa simulasi.

Di dalam makalah ini penyusun akan memberikan contoh penerapan simulasi dengan menggunakan Simulink atau Matlab, yaitu bahasa utama untuk perhitungan teknis, DSP, disain kotnrol, dst. Simulink menyediakan interface grafis ke beberapa fungsi Matlab, sehingga memungkinkan pemakai mendisain model dan mengkontrol sistem secara grafis.

Simulink adalah salah satu bagian dari MatLab. Simulink dapat digunakan untuk mensimulasi sistem artinya mengamati dan menganalisa perilaku dari tiruan sistem. Tiruan sistem diharapkan mempunyai perilaku yang sangat mirip dengan sistem fisik. Jika digunakan dengan benar, simulasi akan membantu proses analisis dan desain sistem. Simulink mendukung simulasi sistem linier, sistem kontrol, sistem yang menggunakan logika kabur, jaringan syaraf tiruan, komunikasi, dan lain-lain.

SEKILAS TENTANG MATLAB

MATLAB (Matrix Laboratory) adalah sebuah program untuk analisis dan komputasi numerik dan merupakan suatu bahasa pemrograman matematika lanjutan yang dibentuk dengan dasar pemikiran menggunakan sifat dan bentuk matriks. Pada awalnya, program ini merupakan interface untuk koleksi rutin-rutin numerik dari proyek LINPACK dan EISPACK, dan dikembangkan menggunakan bahasa FORTRAN namun sekarang merupakan produk komersial dari perusahaan Mathworks, Inc. yang dalam perkembangan selanjutnya dikembangkan menggunakan bahasa C++ dan assembler (utamanya untuk fungsi-fungsi dasar MATLAB).

MATLAB telah berkembang menjadi sebuah environment pemrograman yang canggih yang berisi fungsi-fungsi built-in untuk melakukan tugas pengolahan sinyal, aljabar linier dan kalkulasi matematis lainnya. MATLAB juga berisi toolbox yang berisi fungsi-fungsi tambahan untuk aplikasi khusus . MATLAB bersifat extensible, dalam arti bahwa seorang pengguna dapat menulis fungsi baru untuk ditambahkan pada library ketika fungsi-fungsi built-in yang tersedia tidak dapat melakukan tugas tertentu.

MATLAB (Matrix Laboratory) yang merupakan bahasa pemrograman tingkat tinggi berbasis pada matriks sering digunakan untuk teknik komputasi numerik, yang digunakan untuk menyelesaikan masalah-masalah yang melibatkan operasi matematika elemen, matrik, optimasi, aproksimasi dll. Sehingga Matlab banyak digunakan pada :

Matematika dan Komputansi
Pengembangan dan Algoritma
Pemrograman Modeling, Simulasi, dan Pembuatan Prototipe
Analisa Data , Eksplorasi dan Visualisasi
Analisis Numerik dan Statistik
Pengembangan Aplikasi Teknik

PENERAPAN SIMULINK PADA PENGENDALI PID

PERUMUSAN MASALAH

Sebuah sistem kontrol digambarkan memiliki transfer fungsi / fungsi alih sebagai berikut :

Persamaan fungsi alih tersebut digambarkan dengan sebuah model di dalam Program Matlab dengan Simulink seperti pada rangkaian gambar dibawah ini :

Persamaan tersebut digambarkan pada Program MatLab sebagai berikut :

ps=[1]

qs=[1 15 30]

step(ps,qs)

Dengan hasil respon sistemnya seperti tergambar pada grafik dibawah ini :

Grafik di atas menunjukkan bahwa sistem memiliki kesalahan yang tinggi, hal ini dapat dilihat pada tanggapan sistem menuju ke nilai amplitude. Dari Gambar grafik diatas, dapat juga diketahui bahwa sistem memiliki waktu naik yang lama (hampir mencapai 2 detik). Untuk menghasilkan sistem kontrol yang baik, diperlukan sistem loop tertutup (close loop).

Grafik Respon Awal Sistem

Berdasarkan penggunaan pengendali P, PD, PI dan PID, maka didalam model sistem tersebut dilakukan simulasi untuk mendapatkan aksi pengendali terbaik bagi sistem yang akan diterapkan berdasarkan penggunaan aplikasi yang sesuai didalam proses yang sebenarnya.

AKSI KENDALI PROPORSIONAL (P)

Sesuai dengan dasar pengontrolan, maka aksi kendali Proporsional didapatkan dengan penambahan gain/penguatan sebesar konstanta Proporsional (Kp) sehingga persamaan menjadi :

Dengan menambahkan sebuah konstanta Kp (Proposional) sebesar 300, maka model simulink dapat digambarkan sebagai berikut :

Maka pada Program Matlab dituliskan persamaan-persamaan sebagai berikut :

Kp=300

ps=[Kp]

qs=[1 15 30+Kp]

t=0:0.01:2;

step(ps,qs)

Dengan hasil respon sistemnya seperti tergambar pada grafik dibawah ini :

Penambahan aksi pengendali Proporsional (P) mempunyai pengaruh mengurangi waktu naik dan kesalahan, tetapi konsekuensinya overshoot naik cukup besar. Kenaikan overshoot ini sebanding dengan kenaikan nilai parameter Kp. Waktu turun juga menunjukkan kecenderungan yang membesar.

AKSI KENDALI PROPORSIONAL DAN DERIVATIVE (PD)

Dengan penambahan konstanta Kp (Proposional) dan Kd (Derivative), maka persamaan alih fungsi diatas menjadi :

Apabila dalam sistem diterapkan konstanta Kp sebesar 300 dan konstanta Kd sebesar 10, maka rangkaian gambar di simulink tampak seperti pada gambar berikut :

Dengan menerapkan persamaan pada Matlab seperti dibawah ini :

Kp=300

Kd=10

ps=[Kd Kp]

qs=[1 15+Kd 30+Kp]

t=0:0.01:2;

step(ps,qs)

Maka hasil respon sistem tergambar seperti pada grafik dibawah ini :

Grafik Respon Aksi Proporsional-Derivative (PD)

Pada grafik di atas terlihat bahwa penggunaan kontrol Proposional Derivative (PD) dapat mengurangi overshoot dan waktu turun, tetapi kesalahan tidak mengalami perubahan yang berarti.

AKSI KENDALI PROPORSIONAL DAN INTEGRAL (PI)

Dengan penambahan konstanta Kp (Proposional) dan Ki (Integral) pada sistem, maka persamaan alih fungsi diatas menjadi :

Apabila dalam sistem diterapkan konstanta Kp sebesar 40 dan konstanta Ki sebesar 100, maka rangkaian gambar simulink tampak seperti pada gambar berikut :

Dengan menerapkan persamaan pada Matlab seperti dibawah ini :

Kp = 40

Ki = 100

ps = [Kp Ki]

qs = [1 15 30+Kp Ki]

t = 0:0.01:2;

step(ps,qs)

Maka hasil respon sistem tergambar seperti pada grafik dibawah ini :

Aksi kontrol P dan I memiliki karakteristik yang sama dalam waktu naik dan overshoot. Oleh karena itu, nilai Kp harus dikurangi untuk menghindari overshoot yang berlebihan.

Dari grafik gambar di atas terlihat bahwa waktu naik sistem menurun, dengan overshoot yang kecil, serta kesalahan dapat diminimalkan. Tanggapan sistem memberikan hasil yang lebih baik daripada aksi kontrol sebelumnya tetapi masih mempunyai waktu naik yang lambat.

AKSI KENDALI PROPORSIONAL, INTEGRAL DAN DERIVATIVE (PID)

Dengan penambahan konstanta gabungan ketiga elemen pengaturan : Kp (Proposional), Ki (Integral) dan Kd (Derivative) pada sistem, maka persamaan alih fungsi diatas menjadi :

Apabila dalam sistem diterapkan konstanta Kp sebesar 350, konstanta Ki sebesar 300 dan konstanta Kd sebesar 50, maka rangkaian gambar simulink tampak seperti pada gambar rangkaian berikut :

Sehingga persamaan di dalam Program MatLab berubah menjadi seperti berikut :

Kp = 350

Ki = 300

Kd = 50

ps = [Kd Kp Ki]

qs = [1 8+Kd 15+Kp Ki]

t = 0:0.01:2;

step(ps,qs)

Maka hasil respon sistem tergambar seperti pada grafik dibawah ini :

Grafik Respon Aksi Proporsional-Integral-Derivative (PID)

Dengan aksi kontrol P, I dan D, terlihat bahwa kriteria sistem yang diinginkan hampir mendekati, terlihat dari grafik tanggapan sistem tidak memiliki overshoot, waktu naik yang cepat, dan kesalahan sangat kecil mendekati nol. Grafik tanggapan sistem terhadap sinyal masukan fungsi langkah, tergantung pada nilai parameter Kp, Kd dan Ki.

Dari percobaan di atas dapat ditarik kesimpulan bahwa masing – masing pengendali memiliki karakteristik yang berbeda-beda, antara lain sebagai berikut :

Kontroler (Pengendali) Proporsional (P)

Pengaruh pada sistem :

Menambah atau mengurangi kestabilan

Dapat memperbaiki respon transien khususnya : rise time, settling time

Mengurangi waktu naik, tidak menghilangkan Error Steady State

Untuk menghilangkan Error Steady State, dibutuhkan nilai Kp besar, yang akan membuat sistem lebih tidak stabil.

Kontroler (Pengendali) Integral (I)

Pengaruh pada sistem :

Menghilangkan Error Steady State

Respon lebih lambat (dibandingkan dengan P)

Dapat menimbulkan ketidakstabilan (karena menambah orde sistem)

Kontroler (Pengendali) Derivatif (D)

Pengaruh pada sistem :

Memberikan efek redaman pada sistem yang berosilasi sehingga bisa memperbesar pemberian nilai Kp

Memperbaiki respon transien, karena memberikan aksi saat ada perubahan error.

D hanya berubah saat ada perubahan error, sehingga saat ada error statis D tidak beraksi Sehingga D tidak boleh digunakan sendiri.

Kontroler (Pengendali) Proporsional Integral Derivatif (PID)

Pengendali PID merupakan pengendali yang didasarkan oleh gabungan unsur dari pengendali Proposional (P), Integral (I) dan Derivative (D) yang masing-masing memiliki perilaku yang khas. Setiap kekurangan dan kelebihan dari masing-masing kontroler P, I dan D dapat saling menutupi dengan menggabungkan ketiganya secara paralel menjadi kontroler PID. Elemen-elemen kontroler PID masing-masing secara keseluruhan bertujuan untuk mempercepat reaksi sebuah sistem, menghilangkan offset dan menghasilkan perubahan awal yang besar.

Dengan melihat hasil kesimpulan dari percobaan yang dilakukan, maka dapat dipilih sebuah kontroler (pengendali) yang tepat untuk diterapkan pada sebuah sistem sesuai dengan kondisi proses yang ada.

Disinilah pentingnya sebuah penerapan Simulink untuk melakukan simulasi pada sebuah model sistem dilakukan. Dengan menganalisa hasil respon yang terjadi pada setiap model sistem, dapat diambil sebuah kesimpulan yang akhirnya akan diterapkan pada sistem yang sesungguhnya sesuai dengan keinginan yang akan dicapai.

KESIMPULAN

Ada beberapa cara untuk dapat merancang, menganalisis dan mengoperasikan suatu sistem. Salah satunya adalah dengan melakukan pemodelan, membuat model dari sistem tersebut.

Model adalah alat yang sangat berguna untuk menganalisis maupun merancang sistem. Sebagai alat komunikasi yang sangat efisien, model dapat menunjukkan bagaimana suatu operasi bekerja dan mampu merangsang untuk berpikir bagaimana meningkatkan atau memperbaikinya.

Simulasi merupakan suatu teknik meniru operasi-operasi atau proses- proses yang terjadi dalam suatu sistem dengan bantuan perangkat komputer dan dilandasi oleh beberapa asumsi tertentu sehingga sistem tersebut bisa dipelajari secara ilmiah (Law and Kelton, 1991). Dalam simulasi digunakan komputer untuk mempelajari sistem secara numerik, dimana dilakukan pengumpulan data untuk melakukan estimasi statistik untuk mendapatkan karakteristik asli dari sistem. Simulasi merupakan alat yang tepat untuk digunakan terutama jika diharuskan untuk melakukan eksperimen dalam rangka mencari komentar terbaik dari komponen-komponen sistem. Hal ini dikarenakan sangat mahal dan memerlukan waktu yang lama jika eksperimen dicoba secara riil. Dengan melakukan studi simulasi maka dalam waktu singkat dapat ditentukan keputusan yang tepat serta dengan biaya yang tidak terlalu besar karena semuanya cukup dilakukan dengan komputer. Pendekatan simulasi diawali dengan pembangunan model sistem nyata. Model tersebut harus dapat menunjukkan bagaimana berbagai komponen dalam sistem saling berinteraksi sehingga benar-benar menggambarkan perilaku sistem. Setelah model dibuat maka model tersebut ditransformasikan ke dalam program komputer. Penerapan simulasi dalam program komputer disebut sebagai Simulink.

Sebuah identifikasi masalah selalu dilakukan sebagai tahap awal di dalam sebuah penelitian dan merupakan bagian dari tahap perencanaan (plan). Identifikasi Sistem (Plant) ditujukan untuk mendapatkan sebuah model matematis berupa fungsi alih yang digunakan untuk proses perancangan kontroler nantinya. Sebagai contohnya adalah dalam penerapan Pengendali PID dengan Simulink.

Penggambaran rangkaian awal dengan Simulink sangat diperlukan untuk mempermudah mengamati dan menganalisa perilaku sistem yang telah dimodelkan dalam bentuk model matematis dengan transfer fungsi / fungsi alih. Hingga pada akhirnya hasil akhir dari proses analisa simulasi dengan Simulink tersebutlah yang menjadi bahan dasar dari penerapan ke sistem yang sebenarnya sehingga hasil akhir yang diinginkan dapat terpenuhi dengan baik.